MENTAL vs. La Hipótesis del Universo Matemático de Tegmark

MENTAL vs. LA
HIPÓTESIS DEL
UNIVERSO
MATEMÁTICO DE
TEGMARK

“El universo es una estructura matemática. Solo hay matemáticas; eso es todo lo que existe” (Max Tegmark)

“Todo lo que existe matemáticamente, existe físicamente. Existencia física es equivalente a existencia matemática” (Max Tegmark)

La Hipótesis del Universo Matemático
El cosmólogo sueco-estadounidense Max Tegmark ha desarrollado una “teoría de todo” especulativa, fundamentada en la matemática, que va más allá del platonismo: la Hipótesis del Universo Matemático (HUM), que afirma:

La matemática es lo único que existe.
La matemática, el mundo o cosmos matemático, es lo único que existe, pues es lo más profundo que podemos concebir. La matemática no describe el universo, es el universo.
El universo es una estructura matemática.
Nuestra realidad física externa, es una estructura matemática. Mientras que la física tradicional trata de describir la realidad mediante las matemáticas, la HUM establece que la realidad es matemática, y más específicamente, una estructura matemática. “Todo en nuestro universo es puramente matemático, incluyendo Vd.”. Nuestro universo, con sus leyes particulares, es solo un objeto matemático en el cosmos de las infinitas estructuras matemáticas. Este objeto matemático lo estamos descubriendo poco a poco. La estructura matemática isomórfica a nuestro mundo todavía no la hemos encontrado.

Por la definición de estructura matemática, si nuestra realidad física es isomórfica a una estructura matemática, entonces nuestra realidad física es una estructura matemática. El mundo físico es una estructura matemática abstracta, y las entidades y relaciones de esa estructura matemática abstracta que describe la realidad física, deben ser completamente abstractas.
No hay objetos físicos.
Los objetos físicos son solo estructuras matemáticas que experimentamos a nivel subjetivo. Esta sensación es una ilusión, de la misma forma que experimentamos el color rojo, pues el rojo no es una propiedad del objeto, sino algo concebido por nuestra capacidad cognitiva. “Una estructura matemática es nuestra realidad física externa, más que ser meramente una descripción de la misma”.

Las estructuras matemáticas suficientemente complejas que incluyan subestructuras conscientes de sí mismas −self-aware substructures, SASs−, se percibirán subjetivamente a sí mismas como existentes en un mundo físico “real”. Nosotros somos un ejemplo de tales subestructuras auto-conscientes.
Independencia matemática.
Siguiendo a Platón, sostiene que este universo matemático existe independientemente de nosotros y en él no existe ni espacio ni tiempo. Las entidades de este universo son abstractas e inmutables. Las estructuras matemáticas no han sido creadas, simplemente existen, son atemporales. “No inventamos estructuras matemáticas, las descubrimos, e inventamos solo la notación para describirlas”. La notación matemática carece de importancia. Lo importante son las relaciones que describen.
Libertad.
En el universo matemático no hay leyes en absoluto porque es un espacio de libertad.
La cuestión de Wigner.
Explica la cuestión planteada por Wigner: las matemáticas son tan efectivas para describir la realidad porque son la realidad, porque la realidad es una estructura matemática. El mundo físico es isomorfo a una estructura matemática. La existencia matemática y la existencia física son equivalentes.
Fórmulas.
Las fórmulas o expresiones matemáticas constituyen el mundo matemático manifestado. Es decir, las manifestaciones matemáticas no son los mundos físicos, sino las propias expresiones matemáticas.
Investigación.
En lugar de explorar nuestro universo, que es una estructura matemática particular, es mejor estudiar todas las estructuras del cosmos matemático, el cosmos supremo por una razón: porque es más simple.
Teorías físicas.
Nuestras teorías sobre el universo no son matemáticas aproximándose a la física, sino matemáticas aproximándose a las matemáticas, matemáticas universales reflejadas en matemáticas particulares.
Realidad física externa.
La realidad física externa es independiente de nosotros, los humanos. Al ser la realidad física independiente de los humanos, debería describirse mediante entidades no-humanas, sin conceptos humanos. Debería ser completamente abstracta, sin ningún significado preconcebido. Las únicas propiedades de estas entidades deberían ser las relaciones entre ellas. Es aquí precisamente donde aparece la matemática: en las relaciones.
Estructuras matemáticas válidas.
No todas las estructuras matemáticas existen. Solo existen: 1) Las computables, es decir, las que pueden ser construidas en un número finito de pasos; 2) Las consistentes, es decir, las libres de contradicción; 3) Las decidibles (en el sentido de Gödel), es decir, las que pueden derivarse a partir de un conjunto de axiomas, como los axiomas ZF de la teoría de conjuntos.
Dos perspectivas: la rana y el pájaro.
Hay dos perspectivas o formas de observar la realidad física: la de la rana (o inferior) y la del pájaro (o superior):
- Para el pájaro todo es una estructura matemática eterna e inmutable. El mundo lo ve simple porque percibe lo general. Es la visión del matemático, que solo observa una estructura matemática donde nunca se rompe la simetría. Esta perspectiva superior es lo que ocurre en la teoría de la relatividad de Einstein, en donde todos los eventos ya existen dentro de una estructura matemática llamada espacio-tiempo.
- La rana siente el paso del tiempo. Ve el mundo complejo porque solo percibe los detalles, lo particular, lo superficial. En este nivel, el mundo se describe mediante leyes físicas (leyes del movimiento, ley de la gravitación, etc.). Es la visión del observador dentro de la estructura matemática, donde se rompe la simetría.
TDT (Teoría de Todo).
Una TDT es una estructura matemática completa del mundo físico. Las únicas propiedades de una estructura matemática son las relaciones atemporales e inmutables entre los elementos de la estructura. Como en las estructuras matemáticas no existe el tiempo, tampoco hay “condiciones iniciales”. Tampoco hay aleatoriedad, pues este concepto solo tiene sentido en el contexto de tiempo externo. El universo no es un computador porque no hay nada que computar, pues el universo es una estructura matemática atemporal. Una TDT que incluyese el comienzo de la creación no tendría sentido o sería una descripción incompleta.
Isomorfismo física-matemática.
“Todas las estructuras que existen matemáticamente existen también físicamente”. “Existencia física es equivalente a existencia matemática”. Es el único postulado formulado en “Ultimate Ensemble Theory of Everything” (La teoría definitiva conjunta de todo). Los objetos físicos no son sombras o copias imperfectas de objetos ideales y atemporales pertenecientes a un reino inaccesible sino que son estructuras matemáticas en sí mismas. Esta posición es la contraria del platonismo tradicional.

Hay “democracia matemática”: la existencia física y la matemática son equivalentes. Por lo tanto, todas las estructuras matemáticas tienen el mismo estatus ontológico.
Física cuántica.
No tiene sentido la interpretación de Copenhague (la interpretación de la función de onda como probabilidad), por lo que Einstein tenía razón cuando decía “Dios no juega a los dados”.
Paradoja de Boltzmann.
La paradoja de Boltzmann se aclara en el contexto de la HUM. Esta paradoja se refiere a que, según la segunda ley de la termodinámica, la entropía (el grado de desorden) del universo está siempre aumentando, y sin embargo, observamos orden en el universo porque el universo es una estructura matemática atemporal.

Las implicaciones de la HUM

Según Tegmark, la HUM tiene importantes implicaciones:

Predice la existencia del multiverso (los universos paralelos). Paradójicamente, “Describir un multiverso podría ser más sencillo que describir un único universo”. “Sin el multiverso, la explicación de la realidad se volvería muy complicada y arbitraria”. Si existen muchos universos paralelos, entonces deberíamos encontrarnos en uno normal, típico. Si observamos algo atípico o especial en nuestro universo, podríamos decir que la HUM no es cierta.
Predice que quedan por descubrir muchas regularidades matemáticas a las ya descubiertas, como el modelo estándar de la física de partículas.
La HUM implica la “Teoría de Todo” (TDT), el Santo Grial de la física teórica: una descripción completa de la realidad. “La teoría de todo deberá ser puramente abstracta y matemática”.
Si la HUM es cierta, se unificaría la física y la matemática, y nos permitiría comprender la unidad esencial de todo.

El multiverso

Existen varias teorías o modelos del multiverso. Hay tres que corresponden a universos paralelos no comunicados entre sí. Tegmark añade una cuarta teoría: la hipótesis del universo matemático. Los 4 niveles de la jerarquía van de menor a mayor diversidad:

El multiverso formado por regiones diferentes, y distantes entre sí, de nuestro universo surgido del Big Bang. Están incomunicados entre sí temporalmente porque la luz no ha tenido tiempo de alcanzarlos. Según la teoría de la inflación cosmológica, nuestro universo es infinito.
El multiverso formado por universos que están eternamente incomunicados debido a la inflación cosmológica del espacio. También puede ser el multiverso surgido de varios Big Bangs, donde cada universo podría tener diferentes tipos de leyes físicas, diferentes dimensiones y diferentes tipos de partículas. Puede ser también el multiverso asociado con las ecuaciones fundamentales de la física que tienen más de una solución.
El multiverso de los “muchos mundos” (many worlds), la teoría de Hugh Everett. Cuando se realiza una observación a nivel cuántico, el universo se divide en tantas versiones paralelas de sí mismo como posibilidades existan. Según la interpretación de Copenhague, al realizar una observación, la función de onda se “colapsa”. Pero en la teoría de los mundos múltiples no hay tal colapso, sino que el la función de onda se ramifica y el universo entero se subdivide en tantos universos como posibilidades existan. Todos los universos tienen exactamente las mismas constantes y leyes físicas y la misma estructura del espacio-tiempo, y existen en la estructura matemática abstracta del “espacio de Hilbert”, con infinitas dimensiones espaciales.
El multiuniverso matemático. Nuestro universo es solo una estructura matemática en un cosmos repleto de estructuras matemáticas. Hay muchos universos paralelos, pero son todos objetos matemáticos. Estos universos pueden tener las mismas leyes físicas que el nuestro o tener otras completamente diferentes.

La “Teoria de Todo” (TDT)

Según Tegmark, una TDT debe cumplir varias condiciones:

Debe unificar la teoría cuántica y la teoría de la relatividad general.
Debe ser una estructura matemática simple y de gran belleza. En general, un conjunto es más fácil de generar (mediante un algoritmo) que uno cualquiera de sus miembros. Por ejemplo, el conjunto de los números naturales se puede generar con un programa trivial. En cambio, un número de muchos dígitos y de carácter aleatorio puede tener una enorme complejidad.

Se denomina “complejidad algorítmica” de una entidad matemática al programa más pequeño que lo genera. El “conjunto definitivo” de todas las estructuras matemáticas debe tener la mínima complejidad algorítmica.
Debe basarse en unas estructuras matemáticas sencillas, como los números enteros. De la misma manera que se dice “Todos los caminos conducen a Roma”, todas las estructuras matemáticas deben conducir a unas estructuras básicas y simples.
Debe explicar o describir la visión inferior (la de la rana) a partir de la visión superior (la del pájaro). No podemos verificar la TDT por la visión del pájaro, pero podemos falsar (en el sentido de Popper) la TDT a partir de las observaciones de la rana.

Las SASs

Una SAS (una subestructura autoconsciente) debe cumplir al menos 3 condiciones:

Complejidad. Debe ser compatible con el teorema de incompletud de Gödel.
Predictibilidad. Debe ser capaz de realizar inferencias sobre sus futuras percepciones.
Estabilidad. Debe existir un tiempo suficiente para poder hacer predicciones.

Las SASs son los observadores. Nosotros, los humanos, somos un ejemplo de SAS. Estamos viviendo “dentro” de una estructura matemática. Nos percibimos como algo “local”, estable, permanente, único y aislado. Y nuestra percepción se limita a lo que es útil, estable y permanente.

La estructura matemática que describe nuestro mundo debe ser la más genérica que es consistente con nuestras observaciones. Nuestras observaciones son las más genéricas que son consistentes con nuestra existencia.

La visión de la rana es la forma que percibe una SAS dentro de una estructura matemática. La visión del pájaro es la del matemático que percibe la estructura matemática. Diferentes SASs pueden percibir diferentes realidades físicas.

La autoconciencia sería meramente un efecto lateral de un proceso de información avanzado.

Las SASs deben existir en el espacio-tiempo:

El espacio debe ser de dimensión n=3. Según Paul Ehrenfest [1917], en un espacio de n>3 ni los átomos ni las órbitas planetarias serían estables. Y con n<3, no podría haber fuerza gravitacional y los organismos tendrían serios problemas de tipo topológico (por ejemplo, dos nervios no podrían cruzarse).
El tiempo debe ser de dimensión m=1. De no ser así, se eliminarían ciertas restricciones físicas y las leyes físicas serían diferentes, incluyendo la posibilidad de causación inversa.

El concepto de estructura matemática

Una estructura matemática S es un conjunto de entidades abstractas S₁, S₂, ... con una relaciones abstractas R₁, R₂, .... Por ejemplo, los números enteros, los números reales, los grupos, etc.

Un ejemplo de estructura matemática es el grupo formado por dos elementos (0 y 1) y 4 relaciones definidas mediante una operación (denotada por “+”) definida mediante las expresiones 0+0=0, 0+1=1, 1+0=1, 1+1=0

Esta estructura matemática es puramente abstracta, pudiendo tener diferentes significados concretos. Por ejemplo, “0” puede significar “número par”, “1” “número impar”, y “+” “suma aritmética”. Los símbolos son meras formas sin significado intrínseco. Las relaciones entre los elementos son propiedades intrínsecas. La notación es irrelevante; lo importante son las relaciones abstractas. Por ejemplo, se puede referir al número 4 de diferentes formas: “IV”, “cuatro”, “four”, etc.

Características de las estructuras matemáticas:

Una estructura matemática particular se puede definir como una clase de equivalencia de todas las posibles descripciones o interpretaciones.
Una estructura matemática es una descripción de sí misma, independientemente de la notación utilizada.
Una estructura matemática está libre de descripción humana, de bagaje humano, por lo que no afirma nada.
Por la definición de estructura matemática, si existe un isomorfismo entre una estructura matemática y otra, ambas son la misma estructura.
Una estructura matemática S es reducible si sus entidades se pueden dividir en dos conjuntos T y U sin relaciones entre las entidades de conjuntos diferentes. Los conjuntos T y U son universos paralelos de nivel IV. La mayoría de las estructuras matemáticas (los números enteros, el espacio euclìdeo, etc.) son irreducibles. Un ejemplo de estructura reducible es un conjunto de elementos, que no tienen relaciones entre sus elementos.
Dadas dos estructuras matemáticas, es posible definir siempre una estructura que sea la unión de ambas, con sus correspondientes relaciones. Por lo tanto, un número finito de universos paralelos pueden considerarse pertenecientes a una estructura matemática superior. Desde el punto de vista de la rana, es irrelevante si la estructura matemática forma parte o no de una estructura reducible. Desde el punto de vista del pájaro, lo que importa es la estructura superior.
Un automorfismo de una estructura matemática S se define como una permutación de los elementos de S que preservan todas sus relaciones. Es fácil ver que el conjunto de todos los automorfismos de una estructura S − Aut(S) forman un grupo. Aut(S) se puede considerar como el grupo de simetrías de una estructura, es decir, las transformaciones que hacen invariante la estructura. Las leyes de la física son invariantes bajo Aut(S).

Observaciones:

No todos los universos imaginables existen, pues hay cosas que podemos imaginar que no tienen estructura matemática.
Una estructura matemática no es una teoría.
El multiverso de nivel IV no es el conjunto de todas las estructuras matemáticas.
Una sentencia del lenguaje natural que implique relaciones no es una estructura matemática a menos que obviemos todas las connotaciones o bien añademos entidades y relaciones que la describan con exactitud.

La Hipótesis de la Realidad Externa (HRE)

La Hipótesis de la Realidad Externa afirma que existe una realidad física completamente independiente de nosotros, los humanos.

LA HRE no está universalmente aceptada. La rechazan, entre otros:

Los solipsistas. El solipsismo es una forma radical de subjetivismo según la cual solo existe o solo puede ser conocido el propio yo.
Berkeley. La única realidad es la mental; no hay realidad física.
Los físicos que aceptan la interpretación de Copenhague de la física cuántica: el mundo deja de existir cuando no se le observa.

La Hipótesis del Universo Computable (HUC)

La hipótesis del universo computable se pregunta si nuestra realidad física externa es una forma de simulación por ordenador, y afirma que:

La estructura matemática que es nuestra realidad física es definible mediante funciones computables.
Solo existen físicamente las estructuras matemáticas computables, es decir, que sus resultados se obtienen en un número finito de pasos. Dicho desde otra perspectiva, solo existen físicamente las estructuras matemáticas decidibles, es decir, las que son derivables a partir de un cierto conjunto finito hipotético de axiomas primarios. Esto puede explicar por qué nuestras leyes físicas parecen ser tan simples.
Las relaciones entre las entidades de una estructura matemática son computaciones que no implican el tiempo físico y no hacen evolucionar el universo, sino que solo describen el universo y su historia. Por ejemplo, en la teoría de la relatividad, el tiempo es una variable más, al mismo nivel que las variables espaciales.
Es posible simular nuestro universo mediante un pequeño programa de ordenador.

La HUC elimina paradojas potenciales relacionadas con el nivel IV del multiverso. El multiverso completo de nivel IV, es decir, la unión de las infinitas estructuras matemáticas computables no es una estructura computable, es decir, no es un miembro de sí mismo.

Según Tegmark, las estructuras matemáticas y las computaciones se describen mediante sistemas formales. Pero Tegmark reconoce que estos 3 aspectos −estructuras matemáticas, computaciones y sistemas formales− son diferentes aspectos de una estructura subyacente trascendente “cuya naturaleza no entendemos totalmente”.

Relaciones entre la HUM y otras teorías

Aparte de ser una forma de platonismo radical, la HUM tiene estrechas conexiones o analogías con:

El concepto de MindScape de Rudy Rucker [1982].
El MindScape es un mundo platónico de ideas separadas de lo mental y lo físico. La conciencia explora este mundo o “paisaje mental” que contiene todos los posibles pensamientos. Todos los humanos compartimos este espacio, de la misma manera que compartimos el universo físico.
El “realismo modal” de David Lewis.
Lewis sostiene que los mundos posibles son tan reales como nuestro propio mundo. Todos los mundos posibles tienen el mismo nivel ontológico. Hay infinidad de mundos posibles −el nuestro, uno de ellos−, todos incomunicados entre sí, sin vínculos espaciales, temporales o causales.
El concepto “pi in the sky” de John Barrow [2001].
Barrow utiliza la expresión “pi in the sky” (π en el cielo) con un doble sentido, porque se pronuncia igual que “pie in the sky” (pastel en el cielo). Esta última expresión significa una idea, proyecto, plan, pensamiento o sueño que probablemente nunca se hará realidad por ser inalcanzable.

Para Barrow, las matemáticas son una colección de todos los infinitos posibles modelos o patrones del universo. Las matemáticas son infinitas y están en todas partes. Barrow utiliza la frase “pi in the sky” para explorar el mundo de las matemáticas: su origen, lo que es, si es algo ya existente que descubrimos o si es una invención humana, y si nos puede conducir al significado último del universo.
El “principio de fecundidad (or de plenitud)” de Robert Nozick [1983].
El principio de fecundidad es un principio igualatorio o simétrico. Afirma que todas las posibilidades se realizan o instancian. Ninguna posibilidad tiene un estatus ontológico privilegiado. Todas las posibilidades se dan por igual. Nuestro mundo es solo uno entre los infinitos mundos posibles, coexistiendo con todos ellos.

A su vez, el principio de fecundidad es un principio posible. Por lo tanto, también es realizado o instanciado. Es una instancia de sí mismo. Es un principio que se justifica a sí mismo.
El concepto filosófico de “realismo estructural universal”.
El realismo estructural es aceptar como real el contenido estructural y matemático de nuestras teorías científicas. Solo la estructura del mundo es cognoscible, no su naturaleza. El realismo estructural es el realismo estructural extendido al universo entero. La HUM corresponde a la versión óntica de este concepto, es decir, lo que existe. La HRE corresponde a la versión epistémica, es decir, lo que podemos conocer.

La Triada Matemática – Materia – Mente (MMM)

Según Roger Penrose [2006], existen relaciones entre matemática, materia y mente, que reflejó en un diagrama triangular y circular que se denomina “diagrama de Penrose” o “diagrama MMM”:

Las 3 relaciones son:

La matemática surge o es un producto de la mente.
La materia puede explicarse en términos de la matemática.
La mente surge de la materia.

Este triángulo de Penrose ha sido cuestionado o matizado por Tegmark y otros dos autores (Piet Hut y Mark Alford) en el artículo “On Math, Matter and Mind” [2006], que plantean 3 visiones diferentes:

La visión fundamentalista de Tegmark

Rechaza la flecha “Mente → Matemática”. La matemática no es un producto de la mente humana porque la matemática es independiente del observador humano.

Defiende la flecha “Matemática → Materia” porque el mundo es intrínsecamente matemático, y además la matemática y la existencia física son equivalentes.

Defiende la flecha “Materia → Mente”. La mente y la conciencia surgen de la materia, de ciertos sistemas físicos complejos que procesan información. La mente humana emerge de la materia como una subestructura matemática autoconsciente.

La visión secular de Alford

Defiende la flecha “Mente $rarr; Matemática”. La matemática es una actividad de la mente. Surge de la mente, no de un mundo ideal o superior independiente de nosotros. Rechaza la flecha “Matemática → Materia”. La matemática no es la última sustancia del mundo. Rechaza la flecha “Materia → Mente”. Los procesos mentales no son procesos materiales. La materia es menos fundamental que la mente. No hay dualidad o separación entre mente y materia, sino que son dos aspectos de una misma realidad.

La visión mística de Hut

Cuestiona o rechaza las 3 flechas del diagrama de Penrose por superficiales. Sostiene que se necesita una visión más profunda, unificadora y trascendente. La ciencia siempre ha avanzado en la línea de la unificación. Por ejemplo, en física ha descubierto conexiones intrínsecas entre electricidad y magnetismo, entre espacio y tiempo, entre materia y energía, etc. En este sentido, matemática, mente y materia no son 3 conceptos independientes, y deben unificarse en el futuro. Las flechas del diagrama MMM se deben considerar solo como indicadores de correlaciones significativas, no como relaciones causales. Solo son como las sombras sobre la pared de la caverna de Platón.

MENTAL vs. La Hipótesis del Universo Matemático de Tegmark
La idea de que el universo es matemático se remonta a los pitagóricos de la antigua Grecia. Para Platón, las matemáticas existen en un plano superior o ideal de la realidad. Galileo decía que “El libro de la naturaleza está escrito en el lenguaje de las matemáticas”. Eugene Wigner en su famoso artículo de [1960] se preguntaba por “la irrazonable efectividad de las matemáticas en las ciencias naturales”, que demandaba una explicación. Tegmark va más allá al identificar platonismo matemático con realidad física.

Existen ciertas diferencias entre la hipótesis del universo matemático de Max Tegmark, y MENTAL:

Fundamento.
La posición de Tegmark es especulativa, sin fundamento concreto. En cambio, el fundamento de MENTAL es el principio de causalidad descendente y los arquetipos primarios o dimensiones de la conciencia.

Según Tekmark, existe una estructura subyacente desconocida común a las estructuras matemáticas, a las computaciones y a los sistemas formales. Esta estructura es precisamente MENTAL, el lenguaje basado en arquetipos primarios.

Aplicando el principio de causalidad descendente, podemos afirmar que existe la jerarquía MENTAL – Mundo Matemático – Mundo Físico:
- MENTAL se manifiesta como como estructuras matemáticas, que son las estructuras de relaciones más simples y eficientes. De hecho, la matemática estudia las relaciones entre las primitivas semánticas universales.
- Algunas de esas estructuras matemáticas se manifiestan en el mundo físico.
Los arquetipos primarios.
Lo más profundo que podemos concebir no es la matemática sino los arquetipos primarios. De ellos derivan (entre otras disciplinas) la matemática y la informática, con sus características descriptivas y operativas, respectivamente. La realidad, a nivel profundo, es abstracta. La realidad, lo concreto, lo superficial, está constituida por manifestaciones de los arquetipos primarios, que conectan todo. Todo lo superficial está conectado a través de lo profundo. La verdadera realidad reside en lo profundo, en lo abstracto. La realidad superficial no es la verdadera realidad.

La realidad física y la mental comparten los mismos arquetipos primarios, que son de naturaleza abstracta y que solo tienen relaciones abstractas entre ellas, relaciones que son también arquetipos primarios.
Materia vs. mente.
Nuestras teorías sobre el universo no son matemáticas aproximándose a las matemáticas, sino arquetipos primarios aproximándose a arquetipos primarios, para reconocer arquetipos comunes. Se trata más bien de una identificación o sincronización entre los niveles físico y mental.
Estructuras vs. expresiones.
Tegmark habla de “estructuras matemáticas”. En MENTAL hay expresiones.
Existencia.
Un objeto matemático existe si podemos construirlo o describirlo a nivel formal mediante los arquetipos primarios de MENTAL. Hay dos formas de existencia de un objeto matemático: el nivel descriptivo (asociado a la conciencia del hemisferio derecho) y el nivel operativo (asociado a la conciencia del hemisferio izquierdo). El nivel descriptivo es más general, y el nivel operativo es más particular. Los números irracionales son inaccesibles desde el punto operativo porque son incomputables en un número finito de pasos. Solo algunos de ellos son expresables a nivel descriptivo.

En MENTAL toda expresión es una computación porque toda expresión se evalúa y produce un resultado, que puede ser la propia expresión.

El universo matemático es infinito. Nuestro universo refleja una estructura matemática particular.
Distinción general-particular.
En MENTAL se distingue entre estructura matemática general (que contiene algún parámetro) y las manifestaciones de esa estructura matemática general, que son estructuras matemáticas particulares.
Relaciones.
En MENTAL, la clave reside en las relaciones entre los elementos. Los nombres son irrelevantes. Lo importante son las relaciones. Por ejemplo, la expresión abc es la relación entre tres elementos definida por la secuencia (a b c).
La meta-expresión universal.
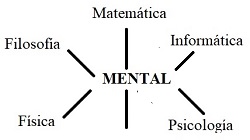
Ω, el conjunto de todas las posibles expresiones, no es una expresión. Por eso se dice que es una meta-expresión, por lo que no se incluye a sí misma. El “MENTALverso” es el universo de todas las posibles expresiones de MENTAL. Por lo tanto, el MENTALverso es Ω.
Grados de libertad.
Los grados de libertad son las primitivas semánticas universales, los arquetipos primarios. Pero existen axiomas que relacionan estas primitivas entre sí. La exploración de todas las posibilidades del mundo matemático es la exploración de todas las posibilidades de MENTAL.
Platonismo.
El universo matemático es de tipo platónico, en el que no existe ni espacio ni tiempo físicos, pero si existe el espacio y tiempo abstractos. Y, por lo tanto, existe el tiempo computacional, que se manifiesta a nivel físico como tiempo físico, por lo que el universo está computando a nivel profundo y manifestándolo superficialmente como movimientos y procesos físicos. Los procesos físicos se pueden considerar computaciones.
Universo físico.
Nuestro universo físico es reflejo o manifestación del universo matemático. Sus leyes y propiedades son matemáticas, pero no es un objeto matemático. El universo es, en lo profundo, de tipo matemático. Pero la matemática no es el último nivel de realidad. El último nivel de realidad reside en los arquetipos primarios. Solo se manifiestan a nivel físico las leyes matemáticas que son descriptivas y operativas.
Invención y descubrimiento.
La matemática es un descubrimiento y a la vez una invención, pues hay muchas formas o paradigmas de acercarnos al mundo matemático.
La cuestión de Wigner.
Las matemáticas son tan efectivas para describir el mundo físico porque este mundo físico es una manifestación del matemático. La realidad no es una estructura matemática, sino una manifestación a nivel físico de una estructura matemática. Mundo físico y mundo matemático comparten los mismos arquetipos primarios.
No-isomorfismo.
No existe identificación entre mundo matemático y mundo físico. El mundo físico es una manifestación del mundo matemático. Solo algunas estructuras matemáticas se manifiestan a nivel físico. No todas se manifiestan. Toda estructura física tiene una estructura matemática subyacente, pero no toda estructura matemática tiene realidad física. La unificación de física y matemática es algo imposible porque la matemática trasciende el mundo físico.

El mundo físico y sus leyes son la referencia sensible que nos permite, mediante un proceso de abstracción, trascenderlo y evocar o conectar con el mundo matemático. Todas las estructuras matemáticas posibles ya existen a nivel platónico, pero solo algunas de ellas se manifiestan a nivel mental o físico.
La rana y el pájaro.
Para la rana el mundo es complejo porque lo percibe desde lo superficial y particular. Para el pájaro, el mundo es sencillo, pues lo percibe desde lo general y universal. MENTAL une o conecta la visión de la rana y el pájaro: lo particular es una manifestación de lo universal. Todas las cosas están conectadas a nivel profundo, a nivel metafisico, donde no hay espacio ni tiempo.
TDT.
MENTAL es una TDT porque todas las cosas comparten los arquetipos primarios, incluyendo el mundo físico, el mental, el mundo matemático y los mundos posibles. Es una TDT de una gran simplicidad, y donde cada primitiva tiene su correspondiente opuesta o dual.
Conciencia.
Para Tegmark, la conciencia surge de la complejidad de las subestructuras matemáticas. Es justamente lo contrario: la conciencia reside en los arquetipos primarios que unen los opuestos o duales. Es imposible que una estructura matemática sea autoconsciente. Pero toda estructura matemática, sea simple o compleja, refleja o manifiesta los arquetipos de la conciencia.
El infinito.
Nada en el mundo físico corresponde al concepto de infinito. La presencia del infinito en las teorías físicas se desecha porque se interpreta como un error o defecto de la teoría.
HRE.
La HRE es falsa. La realidad externa no es independiente de los humanos porque realidad interna (mental) y realidad externa (física) comparten los mismos arquetipos primarios.

La generalización del diagrama MMM

A pesar de la jerarquía mencionada MENTAL-Matemática-Física, todas comparten los mismos arquetipos primarios. El diagrama de las 3 flechas de Penrose es un diagrama que refleja relaciones superficiales. El diagrama que proponemos es reflejo del principio de causalidad descendente: es radial, como el de Piet Hut, pero identificando el elemento central y generalizando la periferia:

En el centro residen los arquetipos primarios, los arquetipos de la conciencia estructurados como el lenguaje MENTAL.
Los extremos de los radios son las diferentes manifestaciones de los arquetipos primarios estructuradas como las diferentes disciplinas: matemática, física, psicología, filosofía, lingüística, etc.

Este diagrama −que podemos denominar “MENTAL-céntrico”− es más simple y más genérico que el de Penrose. Y según el principio de la navaja de Occam, tiene más probabilidades de ser verdadero.

Adenda
El conjunto de Mandelbrot

El paradigma de estructura matemática independiente de los humanos es el conjunto de Mandelbrot, presentado por Benoit Mandelbrot en 1980. Está producido por una fórmula matemática muy simple de tipo recursivo. Somos los exploradores del universo matemático, que es independiente de nosotros, universo en el que se encuentra la estructura matemática platónica que es el conjunto de Mandelbrot, que puede considerarse un universo en sí mismo. La complejidad del conjunto de Mandelbrot solo se encuentra en el borde de la región del conjunto. Según Penrose −en su libro “La Nueva Mente del Emperador”− “El conjunto de Mandelbrot no es una invención de la mente humana; fue un descubrimiento. Como el monte Everest, el conjunto de Mandelbrot está justo ahí”.

Bibliografía

Barbour, Julian. The End of Time: The Next Revolution in Our Understanding of the Universe. The Next Revolution in Physics. Oxford University Press (USA), 2001.
Barrow, John D. ¿Por qué el mundo es matemático? Grijalbo, 1997.
Barrow, John D. Teorías del todo. Hacia una explicación fundamental del universo. Crítica, 2006.
Barrow, John D. La trama oculta del universo. Contar, pensar y existir. Crítica, 2001. Versión española de “Pi in the Sky. Counting, thinking and being”.
Barrow, John D. El libro de la nada. Crítica, 2009.
Barrow, John D. El libro de los universos. Crítica, 2012.
Changeux, Jean-Pierre; Connes, Alain. Materia de reflexión. Tusquets, Colección Metatemas, 1993.
Changeux, Jean-Pierre; Connes, Alain. Conversations on Mind, Matter, and Mathematics. Princeton University Press, 1998.
Ehrenfest, Paul. In What Way Does It Become Manifest in the Fundamental Laws of Physics that Space Has Three Dimensions? Proceedings of the Amsterdam Academy vol. 20, pp. 200-209, 1917.
Hut, Piet; Alford, Mark; Tegmark, Max. On Math, Matter and Mind. Foundations of Physics 36: 765–94, 2006. Internet: arXiv:physics/0510188.
Jannes, Gil. Some comments on “The Mathematical Universe”. Foundations of Physics, 39, 397-406, 2009 arXiv:0904.0867.
Lewis, David K. On the plurality of worlds. Wiley-Blackwell, 2001.
Nozick, Robert. Philosophycal Explanations. Harvard University Press, 1983.
Penrose, Roger. El camino a la realidad. Una guía completa de las leyes del universo. Debate, 2006.
Penrose, Roger. Las sombras de la mente. Hacia una comprensión científica de la consciencia. Crítica, 2007.
Penrose, Roger. Lo grande, lo pequeño y la mente humana. Akal, 2006.
Pickover, Clifford A. El Libro de las Matemáticas. Capítulo: La hipótesis del universo matemático. Librero, 2011.
Rucker, Rudy. Infinity and the Mind. Birkhauser, 1982.
Standish, Russell H. Theory of nothing. BookSurge, 2006.
Tegmark, Max. Is the “Theory of Everything” merely the ultimate ensemble theory? Annals of Physics, 270 (1): 1–51, 1998. Internet: arXiv:gr-qc/9704009.
Tegmark, Max. The Mathematical Universe. Foundations of Physics 38 (2): 101-150. Internet: arΧiv:0704.0646. (versión ampliada de Theory of Everything.)
Tegmark, Max. Shut up and calculate. Internet: arΧiv:0709.4024 (versión reducida del anterior).
Tegmark, Max. Los universos paralelos. Investigación y Ciencia, Julio 2003.
Tegmark, Max. Parallel Universes. En Barrow, J.D.; Davies, P.C.W. & Harper, C.L. “Science and Ultimate Reality: From Quantum to Cosmos”, en honor del 90 cumpleaños de John Wheeler. Cambridge University Press, 2003. Internet (arXiv).
TVE, Programa Redes. Entrevista de Eduardo Punset a Max Tegmark, 26 Febrero 2012. Disponible en Internet.
Wigner, Eugene. The Unreasonable Effectiveness of Mathematics in the Natural Sciences. En Communications in Pure and Applied Mathematics, vol. 13, No. I, Febrero 1960. Disponible en Internet.
Wigner, Eugene P. Symmetries and Reflections. MIT Press, 1970.